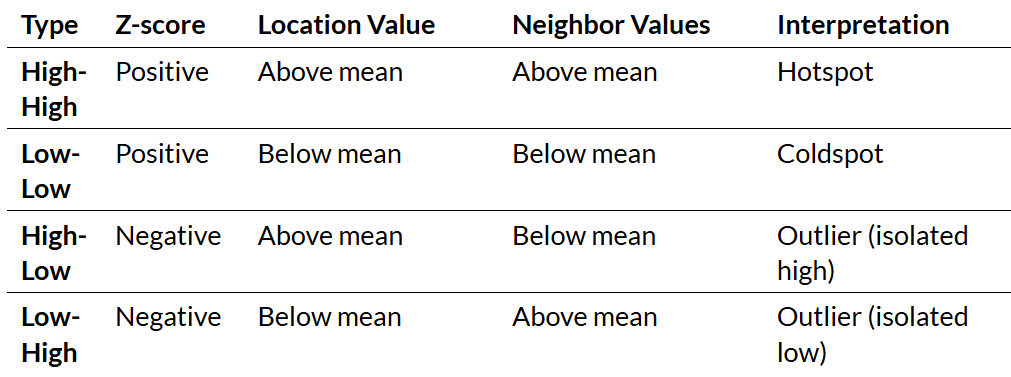
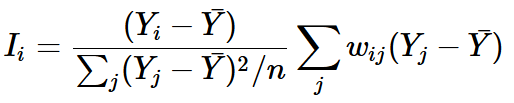Code
library(spdep)
# Step 1: Create spatial object
fishnet_sp <- as_Spatial(fishnet)
# Step 2: Define neighbors (Queen contiguity)
neighbors <- poly2nb(fishnet_sp, queen = TRUE)
# Step 3: Create spatial weights (row-standardized)
weights <- nb2listw(neighbors, style = "W", zero.policy = TRUE)
# Step 4: Calculate Local Moran's I
local_moran <- localmoran(
fishnet$abandoned_cars, # Variable of interest
weights, # Spatial weights
zero.policy = TRUE # Handle cells with no neighbors
)
# Step 5: Extract components
fishnet$local_I <- local_moran[, "Ii"] # Local I statistic
fishnet$p_value <- local_moran[, "Pr(z != E(Ii))"] # P-value
fishnet$z_score <- local_moran[, "Z.Ii"] # Z-score